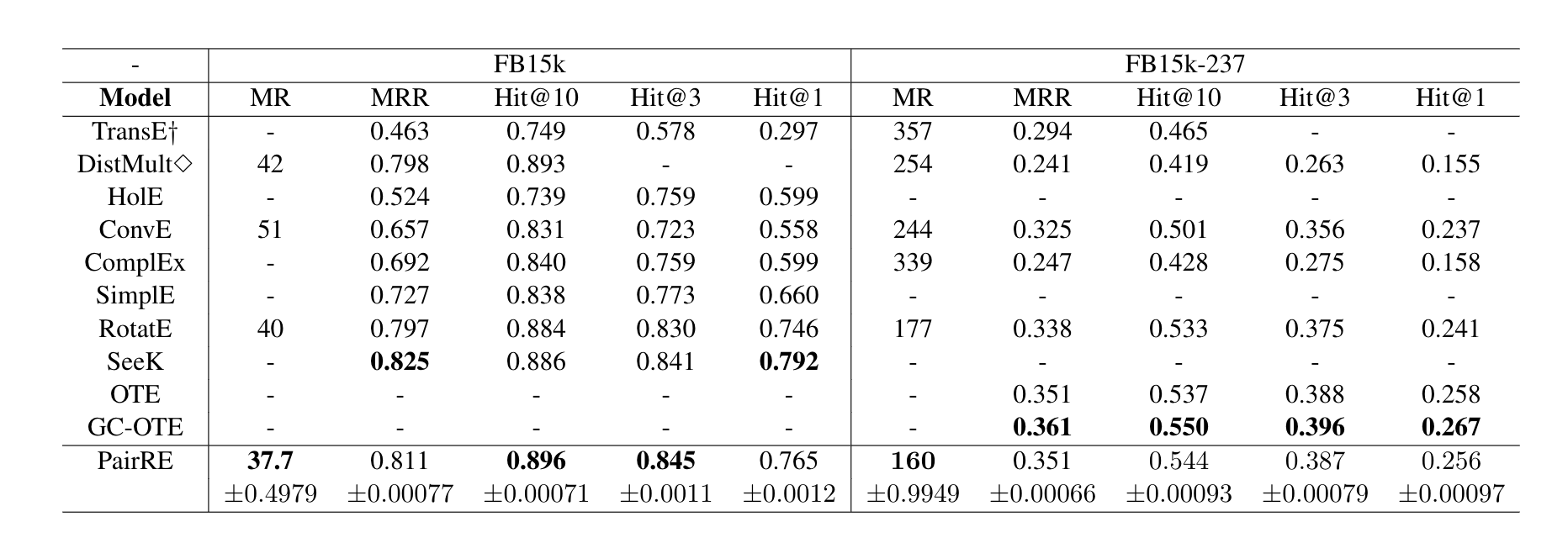
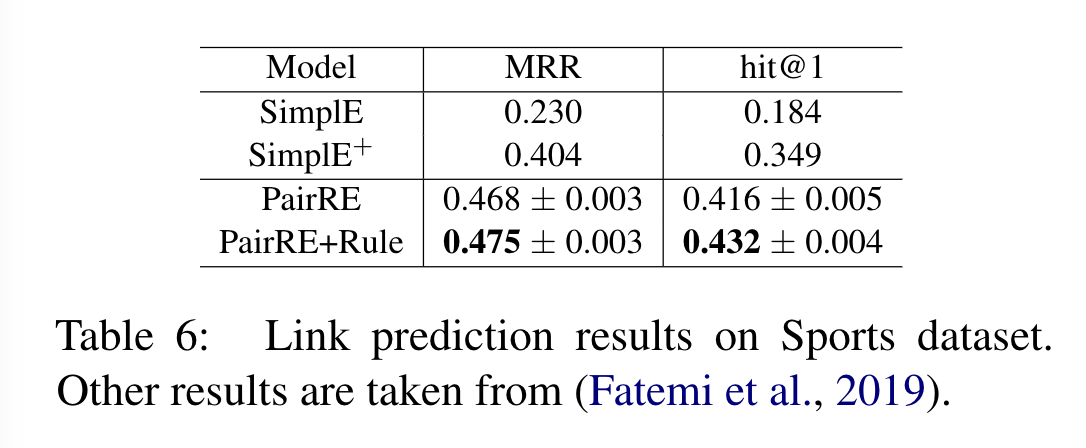
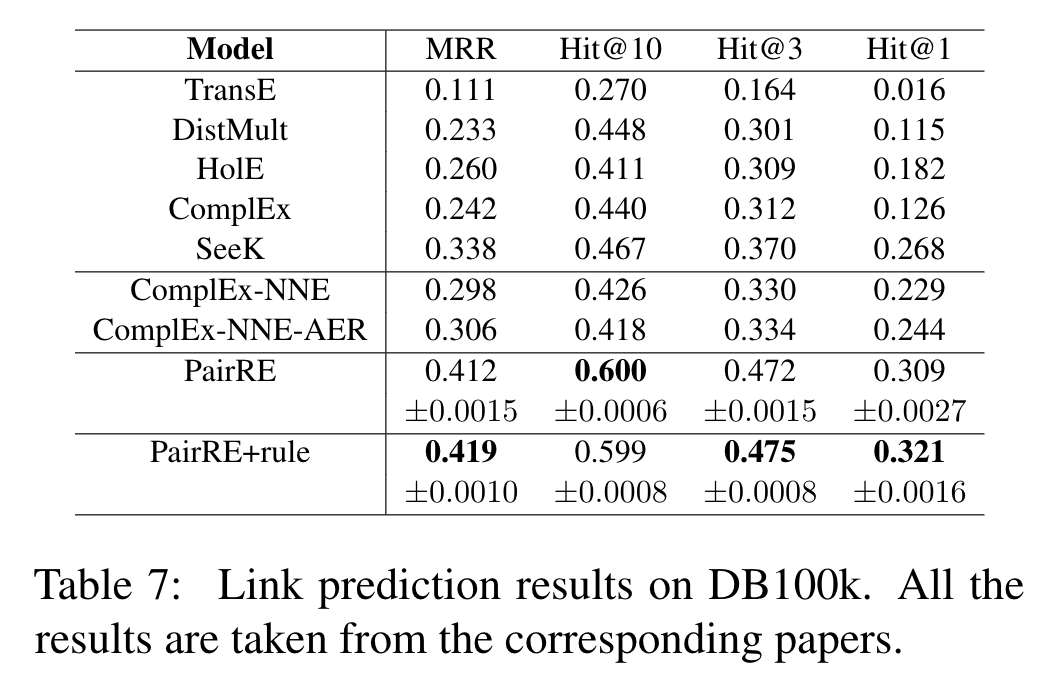
来自蚂蚁,认为现有方法无法同时解决N-to-N问题和关系模式多样性问题,提出了将关系表示为两个向量的PairRE模型。
论文地址:https://aclanthology.org/2021.acl-long.336/
代码:(尚未开源):https://github.com/alipay/KnowledgeGraphEmbeddingsViaPairedRelationVectors
introduction
基于距离的KGembedding方法以TransE为代表,这种方法主要面临两种问题:
- 1-N、N-1、N-N的复杂关系问题中,推理结果往往需要有不同的表示向量
- 学习和建立不同关系pattern,如逆关系、对称关系等
之前的一些方法在一定程度上缓解了这些问题,TransH、TransR、TransD通过使用不同的空间解决复杂关系的问题;RotatE对对称关系、逆关系、组成关系都表现较好。但总体来说复杂关系仍是当前的一大挑战。
formulation
- 统计average number of tails per head(tphr)和average number of heads per tail(hptr)
- 若$tphr\lt1.5,hptr\lt1.5$,则为1-1
- 若$tphr\gt1.5,hptr\lt1.5$,则为1-N
- 若$tphr\gt1.5,hptr\gt1.5$,则为N-N
- 四种关系模式
- Symmetry/antisymmetry: $(h,r,t)<=>(t,r,h)$
- inverse: $(h,r_1,t)<=>(t,r_2,h)$
- composition: $(e_1,r_1,e_2),(e_2,r_2,e_3)=>(e_1,r_3,e_3)$
- sub-relation: $(e_1,r_1,e_2)=>(e_1,r_2,e_2)$,则$r_2$是$r_1$的subrelation
methodology
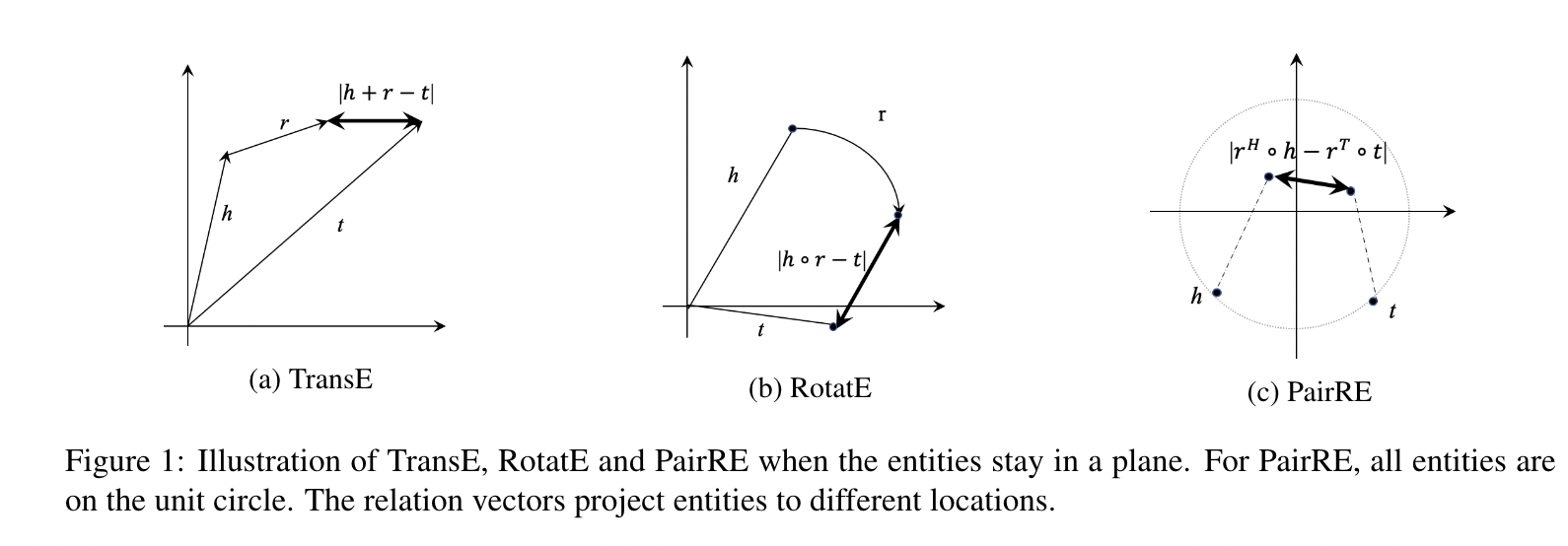
本文提出用一对向量$[r^H,r^T]$表示relation的模型,希望$h\circ r^H = t\circ r^T$。

- scoring func:
$f_r(h,t) = -||h\circ r^H - t\circ r^T||$
其中$||h||^2=||t||^2=1$ - optimization:
- $L=-log\ \sigma(\gamma-f_r(h,t)) - \Sigma^n_{i=1}p(h_t’,r,t_i’)log\ \sigma(f_r(h_i’,t_i’)-\gamma)$
- $p((h_t’,r,t_i’)|(h,r,t))=\frac{expf_r(h_i’,t_i’)}{\Sigma_j expf_r(h_j’,t_j’)}$
- $(h_t’,r,t_i’)$是第i个负样本三元组
文章从公式形式上证明了PairRE编码各种关系模式的能力。
experiment