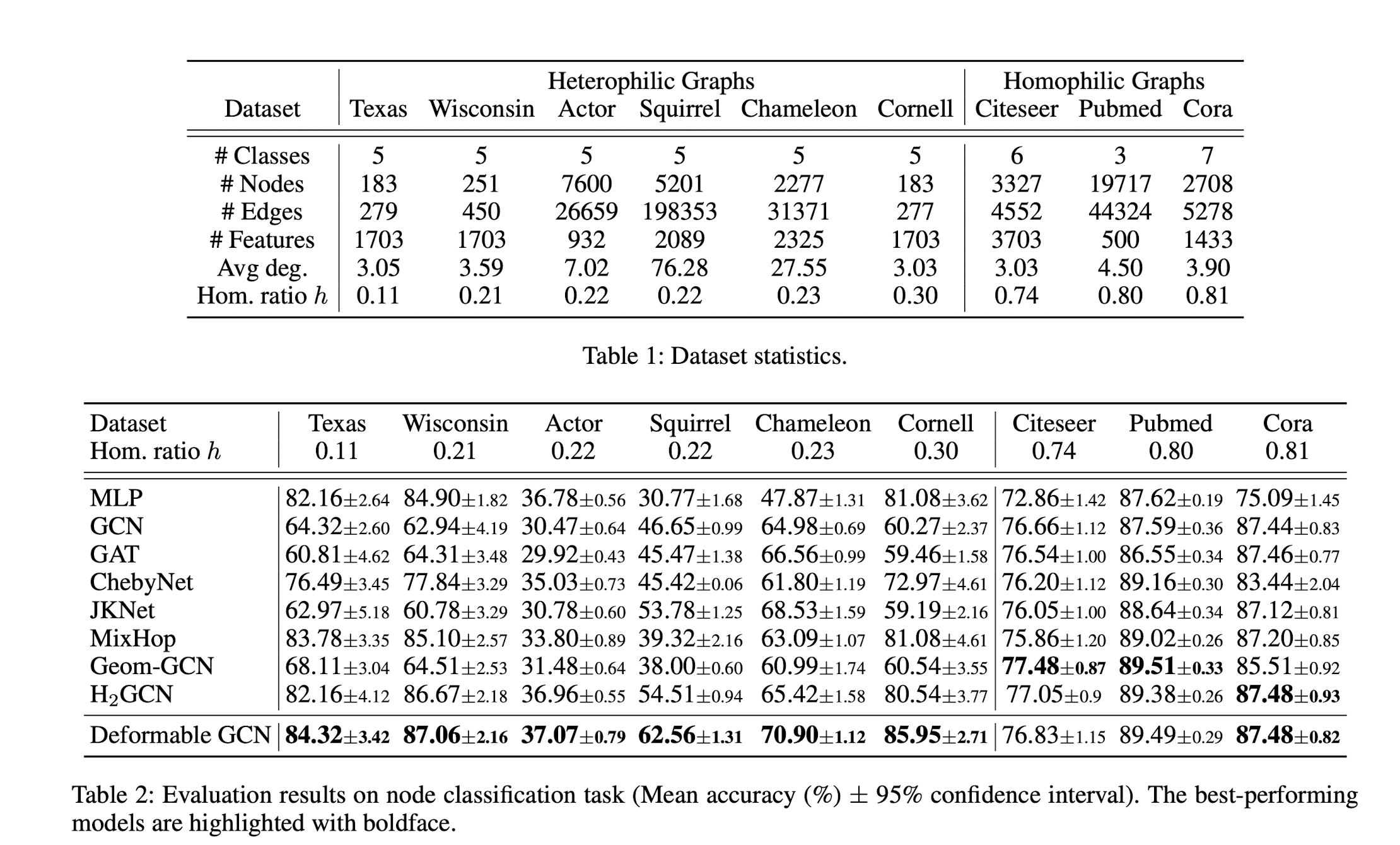
提出在多个潜在空间上进行卷积并根据relation动态调整卷积的方法,并提出了在学习node representation基础上同时学习node positional embeddings的框架。
论文地址:https://arxiv.org/abs/2112.14438
Related Works
limitation of GNN
GCN:$h^{(l)}_v=\sigma(\sum_{u\in \mathcal{N(v)}}(deg(v)deg(u))^{-1/2}\mathbf{W}^{(l)}\mathbf{h}_u^{(l-1)})$
- 图卷积在small的邻域范围内进行,难以捕获长距依赖
- GCN中有相似假设(homophily assumption),邻节点属于不同的类时,聚合信息可能影响效果
GNN会使表示向量更加平滑,是拉普拉斯平滑的一种特殊形式
Deformable convolution
$y_v=(\mathcal{H}*g)(v)=\sum_{u\in \mathcal{N(v)}}g(\mathbf{r}_{u,v})\mathbf{h}_u$
上式中$\mathbf{h}_u\in \mathbb{R}^d$是u的特征,$\mathbf{r}_{u,v}$是u和v的relation,g是随relation变化的线性函数,用于转换特征。
在2D convolution中,$\mathbf{r}_{u,v}=\phi_u-\phi_i$,即u和v的坐标差。而在graph中,$g(\mathbf{r}_{u,v})=(deg(v)deg(u))^{-1/2}\mathbf{W}$,除了normalization外,GCN的线性函数和2Dconv一致。
methods
node positional embedding
对每个node,分别学习node positional embedding和node presentation。node positional embedding用于表示节点位置和相互关系。
node positional embedding是对图节点特征的投影:
$\phi_v^{(l)}=\mathbf{W}_\phi^{(l)}\mathbf{e}_v^{(l)},where\ e_v^{(0)}=x_v,e_v^{(l)}=\frac{1}{\widetilde{deg}(v)}\sum_{u\in \mathcal{N(v)}}e_u^{(l-1)}$
其中$\mathbf{W}_\phi^{(l)}$是要学习的投影矩阵,$\widetilde{deg}(v)$表示带自环的度,$\mathbf{e}_v^{(l)}$表示input经l次smoothing后的输出(应该是指l-layer GCN的输出),每个节点有L+1个node positional embedding。
- 对node position embedding,其他方法诸如LINE、Node2Vec、distance encoding、poincare embedding in hyperbolic geometry也可以应用于此,但本文中简单的node position embedding方法也在模型中取得了很好的效果,因此并没有尝试额外的方法
relation vector
- 用节点u和其相邻节点v的相对位置来表示relation vector
- $r_{u,v}=\begin{cases}[r’_{u,v}||0],&\text{if }\phi_u\ne\phi_v\\
[0,0,\dots,1],&\text{otherwise}\end{cases} \in\mathbb{R}^{d_{\phi}+1}$ - $r_{u,v}’=\frac{\phi_u-\phi_v}{||\phi_u-\phi_v||_2}$
Kernel function
- 线性函数
- $g(r_{u,v})=\Sigma_{k=1}^Ka_{u,v,k}W_k$
$a_{u,v,k}=exp(r_{u,v}^T\tilde{\phi}_k)/Z$
$Z=\Sigma_{u’}exp(r_{u’,v}^T\tilde{\phi}_k)$ - 其中$\tilde{\phi}_k,W_k$都是可学习的参数
- 是K个线性矩阵的加权求和,用于动态的图卷积
- 和dot-product attention 类似(实际上attention也可以看做卷积)
deformable graph convolution
- 利用kernel function为每个邻居都生成了一个转换矩阵,并综合考虑了中心节点v和所有邻居节点u的relation
- $\tilde\phi_k$会通过deformation vector$\Delta_k(e_v)\in\mathbb{R}^{d_\phi+1}$动态调整,在本文中,该deformation vector是用MLP生成的
- Deformable Graph Convolution:
- $y_u=\Sigma_{\mathcal{u\in\tilde N(v)}}g_{\rm deform}(r_{u,v},\Delta_k(e_v))h_u$
- $g_{\rm deform}(r_{u,v},\Delta_k(e_v))=\Sigma_{k=1}^K \hat a_{u,v,k}W_k$
- $\hat a_{u,v,k}=exp(r_{u,v}^T(\tilde{\phi}_k+\Delta_k(e_v))/Z’$
latent neighborhood graph
- DGC是在邻居节点范围内计算的,本文根据该层的input feature用kNN方法寻找邻居节点
- 实际上,根据node position embedding来计算看似更有效,但计算开销太大,且不容易优化
deformable GCN
$\tilde{h}_v=\Sigma_{l=0}^{L+1}s_v^{(l)}\tilde{y}_v^{(l)}$
$s_v^{(l)}=\frac{exp(z^T\tilde{y}_v^{(l)})}{\Sigma^{L+1}_{l’=0}exp(z^T\tilde{y}_v^{(l’)})}$
$\tilde{y}_v^{(l)}=\frac{y_v^{(l)}}{||y_v^{(l)}||_2}$
$z\in\mathbb{R}^{d_v}$是可学习的参数
$s_v^{(l)}$是一种attention,表征邻居u和v是否相配
Loss:
- $\mathcal{L}=\mathcal{L}_{cls}+\alpha\cdot\mathcal{L}_{sep}+\beta\cdot\mathcal{L}_{focus}$
- separating regularizer: $\mathcal{L}_{sep}=-\frac{1}{K}\Sigma_{k_1\ne k_2}||\tilde{\phi}_{k_2}-\tilde{\phi}_{k_1}||_2^2$
- 最大化kernel vector间的距离,从而可以表征不同的relation
- focusing regularizer: $\mathcal{L}_{focus}=-\frac{1}{K\cdot|V|}\Sigma_{v\in V}\Sigma_{k=1}^K||\tilde{\phi}_{k_2}-||\Delta_k(e_v)||_2^2$
- 防止$g_{deform}$发生震荡
experiment