来自国防科技大学,针对关系和头尾实体的联系,提出应该为每个关系r定义一个对头尾实体的滤波器。
论文地址:https://aclanthology.org/2021.emnlp-main.625.pdf
introduction
现有方法基本上都将处于不同的三元组中同一实体表示为相同的向量,实际上,在不同三元组的语义下应该侧重考虑不同的属性。
作者认为,关系在不同的角度描述了头实体和尾实体间的特定属性联系,而衡量三元组是否合理就是比较关系和头尾实体间的语义匹配程度。因此本文提出了语义滤波模块——从不同的三元组中选择实体的不同属性,并设计了基于关系的语义滤波器,从而只提取与关系相关联的语义,抑制其他不需要的维度。
本文从基于MLP的语义过滤器(可以通过特定的regularization转换不大多数几何模型和张量分解模型)出发,设计Linear-2和Diag两种SFBR。
Related work
KG embedding方法分文三类:
- 张量分解模型
- 几何模型
- 神经网络模型
大部分工作都没有对不同三元组中的entity使用不同的表示;TransH、TransR、TransD等做了这方面的尝试,但计算开销很大。
SFBR model
framework
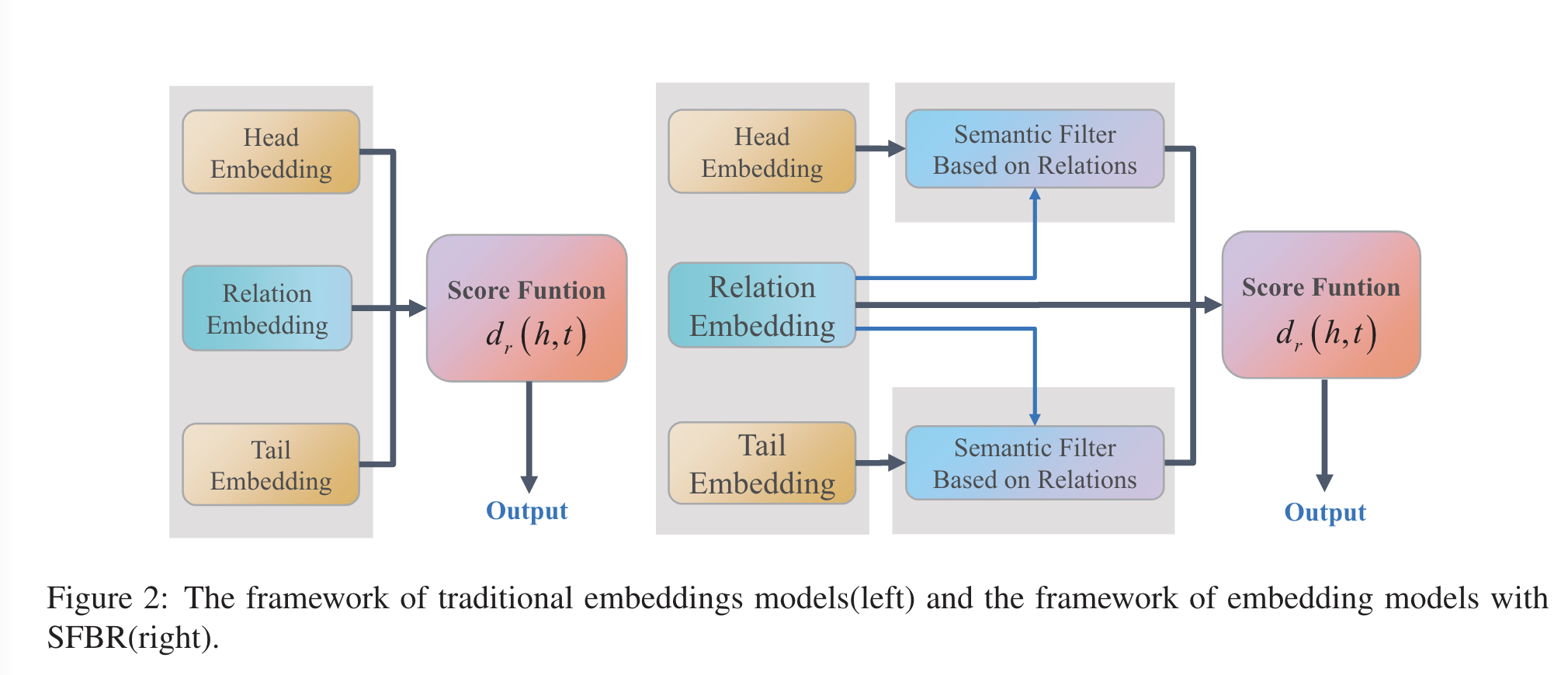
主流模型如上图左,依靠实体和关系唯一的向量表示计算得分。
从人类的角度看,在不同的三元组中,用于计算得分的属性也应该不同。在本文的架构中,作者为实体设计了基于关系的函数,旨在增强实体向量中与关系相关的维度属性,抑制其他维度——类似于信号处理中的滤波器,其公式化表达如下:
- $d_r^f(h,t)=d_r(f_r^h(h),f_r^t(t))$
- 其中$d_r()$是传统的得分函数,$d_r^f是修改后的得分函数$,$f_r()$是语义滤波器
semantic filter module
MLP-filter
$f_r(h)=MLP(h)=hW_r+b$
每个关系都使用一个独立的$f_r$,这样可以确保每个关系滤波器过滤出不同的属性,但是参数量和计算量非常大,本文尝试使用对角化来优化计算。
SFBR Linear-2
作者省去了MLP中的bias,又将$W_r$按分解为四个子方阵后再对角化,减少参数量:
$W_r=\begin{bmatrix}
W_1 & W_2 \\
W_3 & W_4
\end{bmatrix}$
$W_r\in R^{n\times n}, W_1,W_2,W_3,W_4\in R^{n/2\times n/2}$
$W^{linear-2}_r=\begin{bmatrix}
diag(W_1) & diag(W_2) \\
diag(W_3) & diag(W_4)
\end{bmatrix}$
SFBR Diag
为进一步减少参数量,作者将整个$W_r$对角化,以一维向量作为滤波器
$W^{Diag}_r=\begin{bmatrix}
diag(W_1) & O \\
O & diag(W_4)
\end{bmatrix}$
以上的方案中,滤波器的计算公式均为 $f_r(h)=h\odot W+b$
special cases with SFBR
SFBR可以用于扩展各种模型。
- TransE:
- $d_r(h,t)=||h+r-t||$
- $d_r^f(h,t)=||f_r^h(h)+r-f_r^t(t)||$
- RotatE:
- $d_r(h,t)=||h\circ r-t||$
- $d_r^f(h,t)=||f_r^h(h)\circ r-f_r^t(t)||$
- RESCAL
- $d_r(h,t)=||h^TM_rt||$
- $d_r^f(h,t)=||f_r^h(h)^TM_rf_r^t(t)||$
experiment
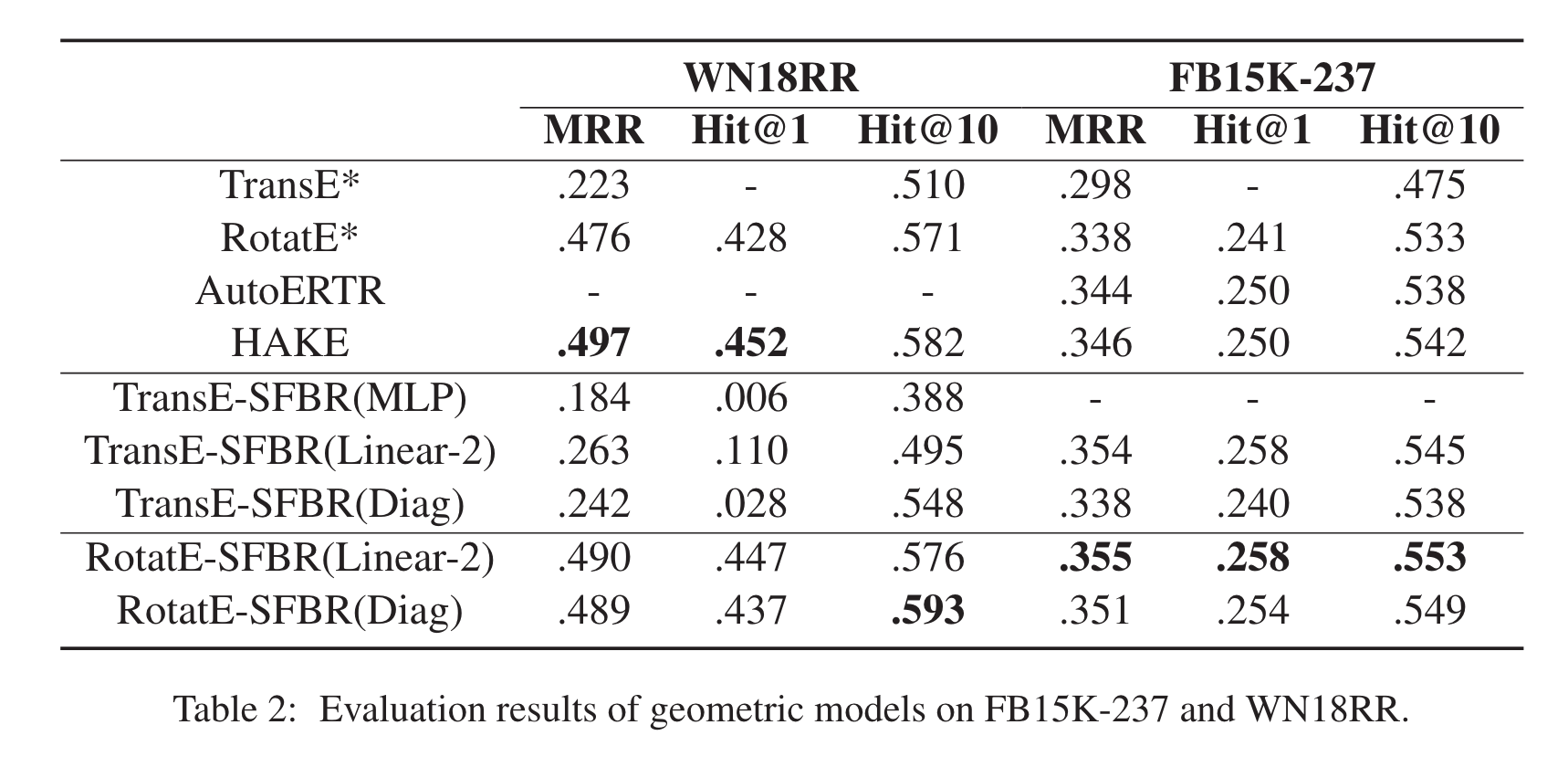
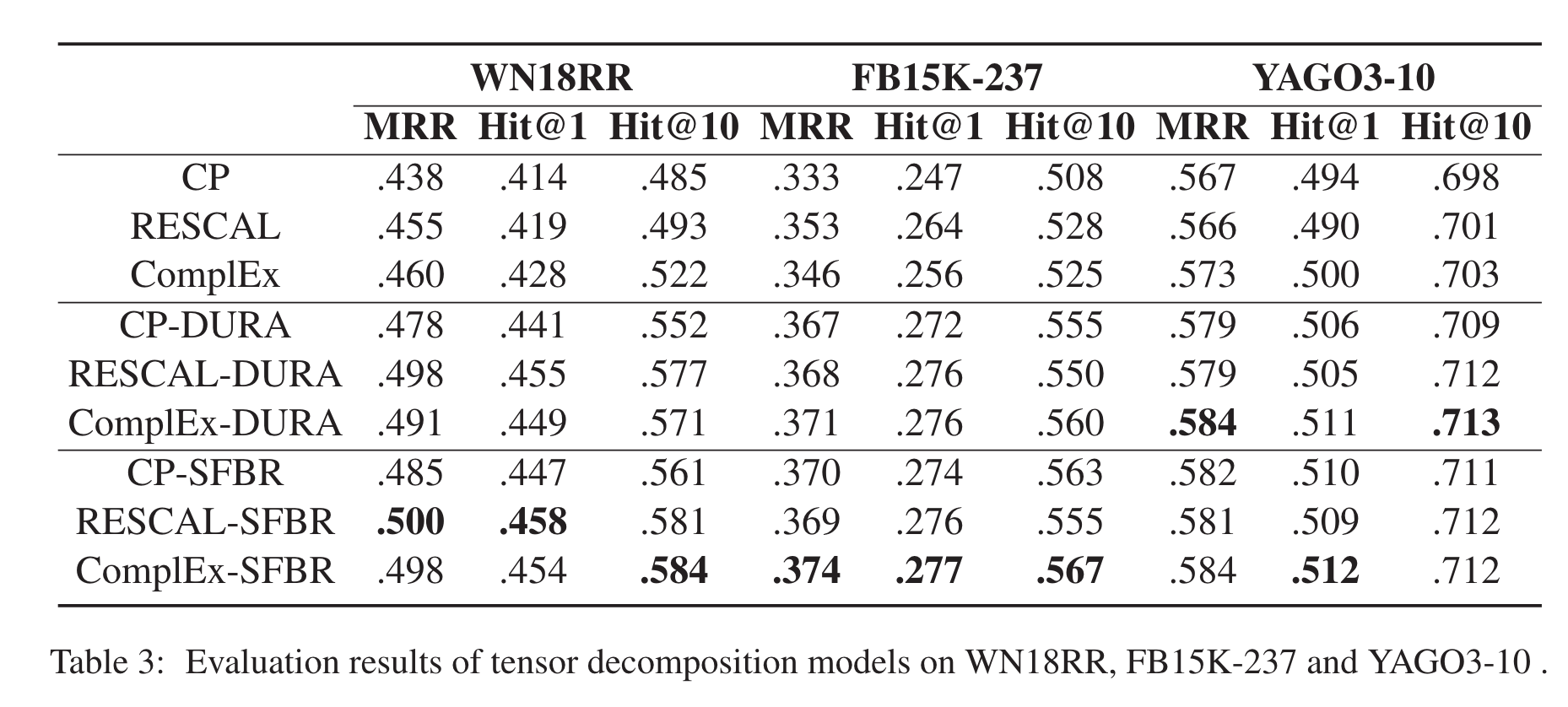
相比张量分解模型和几何模型都有一点点提升。
visualization
