论文链接:Query2Box:Reasoning Over KG in Vector Space Using Box Embeddings
主要思路是(1)将query转换为实体、关系间的逻辑运算;(2)在嵌入空间上定义逻辑运算;(3)用实体和关系的嵌入向量,通过逻辑运算得到query的嵌入向量;(4)定义距离函数,查找离query近(本文为在box中)的实体,即为推理的答案。
Abstract
最近在大规模KG上回答query的一种典型方法是将KG实体和query嵌入到向量空间中,答案实体在嵌入向量空间中会和query很近。
先前工作将query投影成单点,但复杂查询的answer会是一个潜在的大集合。
先前工作只能处理合取$\wedge$和存在$\exists$,对析取$\vee $查询的处理仍未解决。
本文提出的Query2box将query嵌入为box超矩形框,box内的一组点对应于一组答案实体,作者证明了合取可以天然地表示为boxes地交集,但处理析取需要embedding的维度和KG实体数成比例。但是,通过将query转换为析取范式,Query2box能以可扩展方式处理合取、析取和存在逻辑查询。
Introduction
一阶逻辑查询可以表示为有向无环图DAG,并可以根据DAG进行推理,缺点是(1)子图匹配的计算复杂度和query size成指数关系,这会影响到向大规模KG的扩展;(2)子图匹配非常敏感,因为它不能正确地回答缺少关系的查询。为了解决第二个问题,可以对KG中缺失的关系进行补全,但是这样会使得KG更加稠密,这就加剧了第一个问题。
Embedding方法将逻辑查询和KG实体嵌入到低维向量空间中,而答案会在query附近,这种方法可以鲁棒地补全关系,且速度很快,因为回答任意的逻辑查询被简化为了识别在向量空间中最接近于query嵌入向量的实体。

先前工作中(1)将query嵌入到向量空间的单点,而回答一个query需要遍历KG并建立一个active实体集,且如何有效地将一个集合建模成一个单点还是有待研究的。(2)在向量空间中定义两个点的逻辑操作符(例如 集合交集)也是不自然的。(3)只能处理conjuctive queries,是一阶逻辑中的子集,包含合取$\wedge$和存在$\exists$,但不包括析取$\vee$。在向量空间有效地处理析取逻辑还是一个有待解决的问题。
本文中提出的query2box能以可扩展方式处理任意EPFO(Existential Positive First-order)逻辑查询(包含任意$\wedge、\exists、 \vee$的查询)。关键思想是使用向量空间中的封闭区域box而非单点来表示query(Figure1-D),如此(1)Boxes可以自然地对其包含的实体进行建模;(2)逻辑运算符(例如 集合交集)在box上的定义也很自然,就像venn图一样;(3)在box上执行逻辑运算符就会产生新的box,这意味着操作符是封闭的,通过逻辑计算迭代box可以高效地执行推理。
作者证明了query2box可以很自然地处理conjunctive query,也证明了将EPFO查询嵌入到单个点或box中需要与KG实体数量成比例地嵌入向量尺寸,难以实现。本文的解决方案是将EPFO查询转化为析取范式(DNF),将其表示成一组boxes,每个box对应DNF中的一个conjunctive query,再将最近的实体作为查询答案返回,即回答多个EPFO取并集再找最近实体。
(boxes本质上是向量空间中的venn图,但box是和嵌入共同学习的。)
QUERY2BOX: LOGICAL REASONING OVER KGS IN VECTOR SPACE
KNOWLEDGE GRAPHS AND CONJUNCTIVE QUERIES
KG:$\mathcal{G=(V,R),\\ V表示实体,\\ R:V\times V \rightarrow \{true,false\}表示两实体之间是否存在有向边}$
Conjunctive queries: 使用$\exists、\wedge$操作的一阶逻辑查询的子类,表示如下
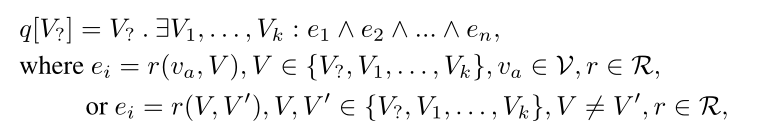
$v_a$表示不变锚实体,$V_1,…,V_k$是量化的边界变量(quantified bound variables),$V_?$ 是目标变量实体。回答查询q的目标是$找到一个实体集[q] \subseteq \mathcal{V} 使得 v\in[q]当且仅当(iff) q[v]=True$,$[q]$就是query的答案集。
从DAG(Figure1-A)可以得到计算图(Figure1-B),其中包含了Projection和Intersection两种计算。
对给定的查询q,计算图将推理过程转换为通过计算得到答案实体集的过程,即从锚节点集合出发,迭代使用两种运算直至到达唯一的目标节点。
REASONING OVER SETS OF ENTITIES USING BOX EMBEDDINGS
到目前为止我们将conjunctive queries定义成了计算图,并且可以直接在KG的节点和边上执行.
给定一个复杂query,将其分解为一系列逻辑运算,并在向量空间中定义逻辑推理执行这些运算,这样将获得查询的嵌入,且查询嵌入box中会包含查询答案。
Box embeddings

$Cen(p)$表示box的中心,$Off(p)$表示box的正偏移(大小)。KG中的每个实体都被表示为为一个$\mathbf{v} \in \mathbb{R}^d$ 即大小为0的box,box的p建模了一个实体集$\{v\in \mathcal{V}:\mathbf{v} \in Box_p\}$ ,即其向量在box内的实体。
本文的框架是基于query的计算图在向量空间中进行推理的,如Figure1-D所示:从初始锚节点的box开始,根据逻辑操作不断更新box的embedding。下边介绍entity-to-box距离函数以及为了学习嵌入和几何操作符(geometric operators)的整体目标函数。
Initial boxes for source nodes
每个源节点表示一个锚实体$v\mathcal{\in V}$,这可以很自然地表示为Cen为v,Off为0的box,即$(v,0)$。
Geometric projection operator
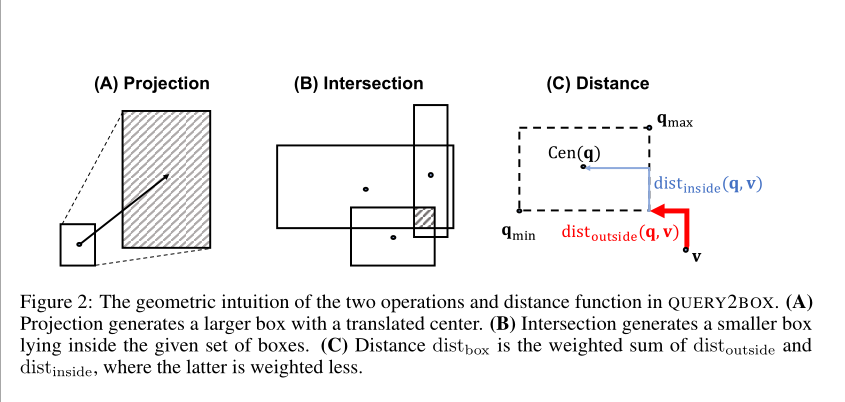
将每个关系$r\in \mathcal{R}$和关系嵌入$\mathbf{r} = (Cen(r),Off(r)) \in \mathbb{R}^{2d}$联系,给定一个输出box embedding $\mathbf{p}$,用$\mathbf{p+r}$表示其projection运算:对Cen和Off分别求和,得到一个中心转移的、大小更大的box,如Figure2-A所示。
Geometric intersection operator
对一组box embeddings$\mathbf{p_1,\cdots,p_n}$,用$\mathbf{p_{inter}} = (Cen(\mathbf{p_{inter}}),Off(\mathbf{p_{inter}}))$表示其intersection运算,对box的中心使用注意力机制,并使用sigmoid函数缩小box的偏移量。

其中$\odot$表示dimension-wise的乘积;$MLP(\cdot): \mathbb{R}^{2d}\rightarrow \mathbb{R}^d$是多层感知机;$\sigma(\cdot)$表示sigmoid函数;$DeepSets(\cdot)$表示排列不变的(permutation-invariant)深层架构;$Min(\cdot), exp(\cdot)$都在dimension-wise进行操作。作者用 $DeepSets({\{\mathbf{x_1}, …, \mathbf{x_N}}\}) = MLP((1/N)\cdot \sum^N_{i=1}MLP(\mathbf{x_i}))$表示所有的deep sets,其中的MLP隐层维度都和输入维度相同。
几何交集运算的思想是在一组box内生成一个小的box,和通常用的deep sets不同,本文的几何交集操作有效地限制了中心的位置并且缩小了set的大小。
Entity-to-box distance
给定一个query box $\mathbf{q} \in \mathbb{R^{2d}}$和一个实体向量$\mathbf{v} \in \mathbb{R^d}$,距离定义为:
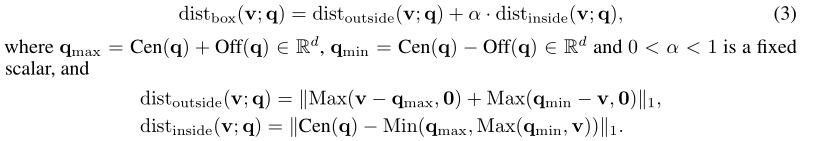
如Figure2-C所示,$\mathbb{dist_{outside}}$对应于实体和其在box内最接近的边/角的距离;$\mathbb{dist_{inside}}$对应于box的中心和它的边/角的距离(如果实体在box内则为实体自身)。
关键在于用$\alpha$降低了$dist_{inside}$的权重,这意味着在box内的实体被视为和box距离足够近,若$\alpha=1$,则距离退化为$L_1$距离,如TransE中用的$|Cen(q)-\mathbf{v}|_1$。
Training objective
模型需要学习实体嵌入以及几何映射和交集操作符。
给定queries和answer的训练集,通过优化负采样损失优化基于距离的模型:
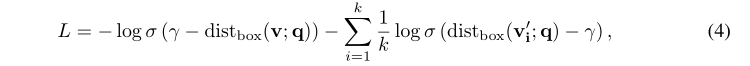
其中$\gamma$表示margin;$v\in [q]$是正实体(query q的答案);$v^{‘}_i \notin [q]$是第i个负实体(非query q的答案);k是负实体的数目。
TRACTABLE HANDLING OF DISJUNCTION USING DISJUNCTIVE NORMAL FORM
增加了一种新类型的有向边Union
一种简单的方法是为union定义几何操作符,如同前面的操作一样。但是对于box embedding有一个挑战:boxes可以位于向量空间中的任意位置,它们的union可以不再是一个简单的box。
作者证明了一个适用于所有通过embedding将query嵌入为$\mathbf{q}$并通过距离查找实体的方法的负面结果。
Theorem 1
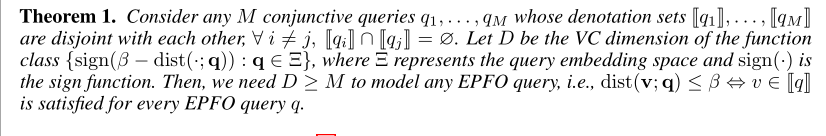
对任意M个不相交的合取查询 $q_1,\cdots,q_M$,D是函数集${sign(\beta-dist(\cdot;\mathbf{q})):q\in \Xi}$的VC维数,其中$\Xi$表示query的嵌入空间,sign为符号函数,那么需要$D\ge M$才能建模任意的EPFO以通过距离寻找答案。
对于真实世界的的KG,有$M \approx \mathcal{|V|}$个不相交的合取查询,这就要求距离函数的VC维度和KG实体数目一样大,因此无法扩展到大型KG/边缘未知的KG。
为了解决这个问题,作者的主要思想是将给定的EPFO query转换为析取范式(DNF)即合取的析取,以使析取操作仅出现在最后一步,从而可以在低维空间中对每个合取查询进行推理。
Transformation to DNF
所有的一阶逻辑都可以转换为DNF,可以直接在计算图的空间进行转换。给定EPFO query q,其计算图为$G_q=(V_q,E_q)$,
$V_{union}\subset V_q$表示入边的类型为“union”的节点集合。对于每个$ v\in V_{union}$,定义$P_v \subset V_q$为其父节点的集合。
首先生成 $N=\prod_{v\in V_{union}}|P_v|$个不同的计算图$G_{q^{(1)}}, \cdots, G_{q^{(N)}}$(步骤如下所示),其中每个在第一步都有不同的$v_{parent}$选择:
- 对每个$v\in V_{union}$,选择一个父节点$v_{parent} \in P_v$
- 删除所有union类型的边
- 合并$v$和$v_{parent}$,并保留所有其他类型的边
然后组合获得的计算图$G_{q^{(1)}}, \cdots, G_{q^{(N)}}$,以得到最终的等价的计算图:
- 将获得的所有计算图的目标汇聚节点转换成量化边界的变量节点(the existentially quantified bound variables nodes);
- 创建一个行额目标汇聚节点$V_?$,从上述所有的变量节点到新的目标节点连接“union”类型的有向边。
整个转化过程如下Figure3所示,该计算图与原始计算图等价。
Aggregation
定义给定EPFO查询$q$ 和实体$v\in \mathcal{V}$ 间的距离函数,因为$q$ 在逻辑上等效于$ q^{(1)}\vee \cdots \vee q^{(N)}$,距离函数很自然地定义为:
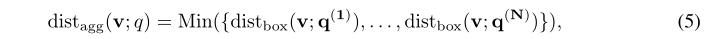
该模型和union操作一致,只要实体在一个集合中,该实体就在集合的union中。
Computational complexity
计算复杂度等同于回答N个交集查询,且这N个查询是可并行的。回答每个conjunctive query的速度很快,因为它执行一个简单的box操作序列,然后在嵌入空间中执行一系列搜索,搜索可以基于局部敏感哈希(LSH)技术在固定时间内完成。