论文链接:Reasoning Like Human: Hierarchical Reinforcement Learning for Knowledge Graph Reasoning
Abstract
KG推理补全的一种流行方法是通过对连接两实体的其他路径上发现的信息来进行多跳推理。当一个关系/实体具有多含义时,效果会显著降低,本文受人类处理认知模糊情况的分层结构启发,提出了层次强化学习框架来自动从KG中学习推理链。
Introduction
本文提出了分层强化学习框架(RLH,Reason Like Human)以模仿人的思维模式,在KG上进行多跳推理。通过模拟分层决策,模型能够自动学习推理的路径链。
模型由一个高级策略和一个低级策略组成,将宏观操作分解成更简单的子任务,从而学习每个关系的潜在语义。
Definitions and Notations
Definition 1 KG
KG是一个有向图$G=\mathcal{(E,R,U)}$,其中$\mathcal{E、R、U}$ 分别为实体集、关系集、边集($(e_o,r,e_t)$)
Definition 2 KG Reasoning
给定三种情况$(h,r,?),(?,r,t),(h,?,t)$,KG Reasoning通过k跳的推理路径($e_1 \xrightarrow {r_1} e_2 \xrightarrow {r_2} \cdots \xrightarrow {r_k} e_{k+1}$)来预测其中的 $?$ 。
Definition 3 Markov Decision Process
马尔可夫决策过程是一个四元组$(S,A,P_a,R_a)$,其中$S$ 是有限状态集,$A$ 是有限行动集($A_s$ 是状态$S$ 下的行动集),$P_a(s,s’)=P_r(s_{t+1}=s’|s_t=s,a_t=a)$ 是$t$ 时间$s$ 状态下采取行动$a$ 会在$t+1$时间到达状态$s’$ 的概率,$R_a(s,s’)$ 是通过动作$a$ 完成$s \rightarrow s’$ 的奖励。
RL是一个MDP,在序列的每一阶段,Agent观察一个环境状态$s$,并执行一个动作$a$,收到一个期望为$R(s,a)$ 的即时奖励和状态转移概率 $P(s’|s,a)$。
Definition 4 Hierarchical Reinforcement Learning
分层强化学习是一个semi-MDP$(S,A,P_a,r_{a,\Phi})$,其中$P_a(s,s’)=P_r(s_{t+1}=s’|s_t=s,a_t=a)\Pi_{i=1}^{K-1}P_r(\phi_{i+1}|\Phi_i)$。$\Phi$ 是一个用来描述动作$a$ 内部的K个转移阶段的转移函数空间,每个$\phi$ 都是$a$ 的一个子动作,所有的$\phi$ 都是相关的。
HRL的每个多做包括时间上离散的、可计数的子动作。HRL将整个问题的优化下发给更简单的子问题,在子问题中知识可以相互传递,重组子问题中的解决方案可以解决更大更复杂的问题。
Methodology
RLH
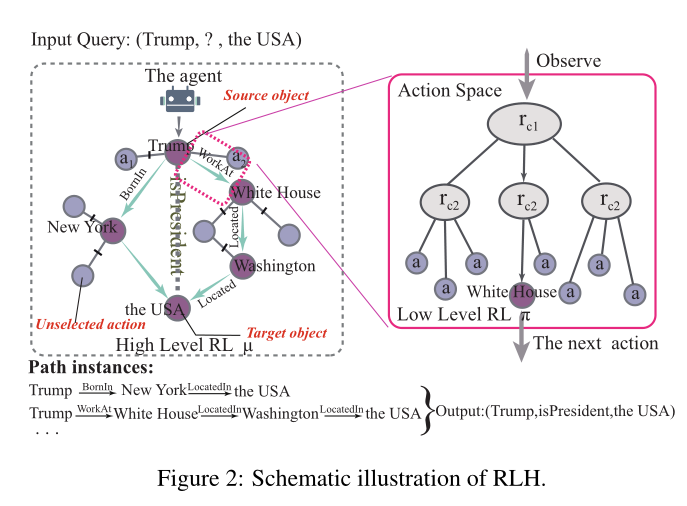
Agent对每个query预测一个源实体到目标实体的路径,它观察当前state并执行分层策略决定下一跳的实体。Agent不断观察并决定下一跳,直至它到达目标实体或最大长度。Agent的轨迹就是一个推理链,可以解释如何从推理系统获得查询结果。
在KG环境中,动作空间通常是层次结构,所以复杂的动作空间就会分解为像决策树一样的子任务,关系的多重语义也被分解为更具体的表示。
High Level Policy for Encoding History Information
RL训练Agent从KG与环境的交互中学习。KG中,RL由四元组$\mathcal{(S,A,P,R)}$ 表示。
States step $i$ 的state表示为$s_i=(e_{i-1},r_i,e_i,e_t)$ ,其中$e_i\in \mathcal{E}$ 表示当前实体,$e_{i-1}$ 表示上一个实体,$r_i$ 表示这两实体间的关系,$e_t$ 是目标实体。给定实体对$(e_o,e_t)$,起始状态为$(‘ST’,’ST’,e_o,e_t)$,终态为$(e_{t-1},r_t,e_t,e_t)$。
Actions 状态$s_i$的行动集是当前实体$e_i$ 的出边集。
Transition 转移$\mathcal{P:S \times A \rightarrow S}$ 是状态转移概率函数,转移策略是选择$\mathcal{P}(s_{i+1}|s_i,a_i)$ 中最大概率的$a_i$。
Policy 高级策略网络$\mu(s,\mathcal{A})=P(a|s;\theta)$ 用于在连续空间中建模RL Agent,$\theta$ 是网络参数。用历史向量$\mathbf{h_t}$ 来保存历史信息进行序列决策。给定步骤$t$ 的轨迹$\tau$,历史向量$\mathbf{h_t}$ 由$\mathbf{h_{t-1}、s_{t-1}}$ 决定
其中$\mathbf{c}$ 是低级策略输出子动作的向量表示,$\mathbf{W_\pi}$ 是Rewards矩阵
Rewards 如果agent到达了目标实体,则每跳的奖励定义如下:
Low Level Policy for Structured Action Space
低级策略$\Phi$ 将复杂动作空间$\mathcal{A_s}$ 分解为结构化的子动作。子动作转换也是一个马尔可夫过程。通过层级聚类的关系嵌入方法,KG中的关系可以形成关系簇,低级RL的所有状态被组织为一个搜索树,可以很好地表达每个关系的潜在多重语义。
Actions 首先执行TransE获得嵌入向量,然后应用k means算法初始化关系簇,构建层次结构的关系簇集。
State 低级状态$s_i$ 包括当前有效子动作集,一个轨迹的起始状态是$A_s$,如果成功则终态为${a_{t+1}}$,否则为$\varnothing$。
Policy Agent观察$s_i^l$ 的子操作空间,执行子任务
其中$c_t$ 是要采用的子动作
Reward 对终态包含正确动作$a_{next}$时获得奖励。
Optimization and Training
低级策略网络的目标函数是最大化层次决策的累计回报
其中$\epsilon$ 表示从低级策略$\mu$ 的潜在分布$p\theta_L(\epsilon)$ 中生成的$M$ 长的轨迹。
高级策略的目标函数是
其中$\epsilon$ 表示从潜在分布$p\theta_H(\tau)$ 中生成的$N$ 长的轨迹。
然后使用 policy gradient methods的 REINFORCE 算法优化两个策略。
