论文链接:Embedding Logical Queries on Knowledge Graphs
主要思路是(1)根据DAG结构表示query,利用$\mathcal{P}$ 算子将起点的嵌入向量集投影到到以$\tau$ 类型的出边连接的相邻节点的嵌入向量集;(2)再用$\mathcal{L}$ 算子对嵌入向量集取交集;(3)重复以上步骤直至全部聚合,得到query的嵌入向量;(4)在嵌入空间中最近邻搜索查找与query最近的节点。
[TOC]
Approach
总体思路
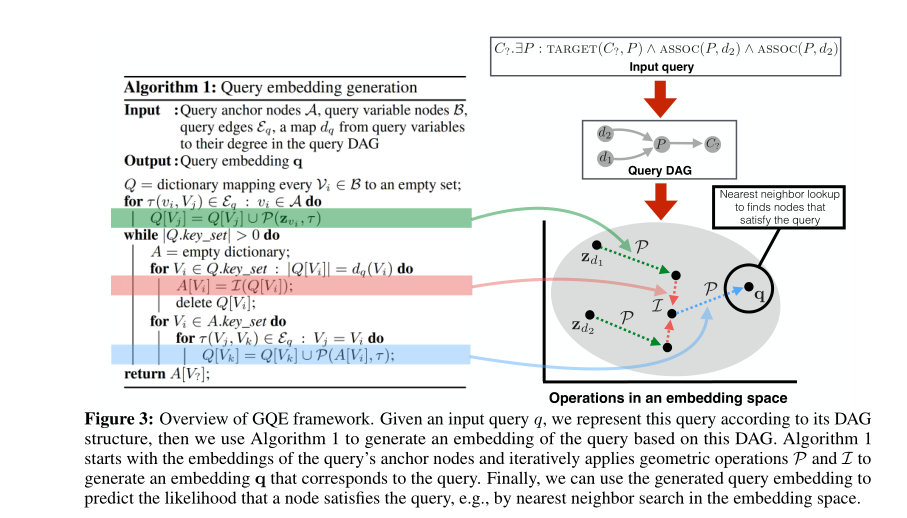
用算子$\mathcal{P, L}$ 将查询$q$ embedding到 $\mathbf{q} \in \mathbb{R}^d$,目标是优化这些算子以用来预测q的回答——节点v。
通过生成query和node的嵌入向量,用距离来表示得分:
目标是生成一个能隐含表示的$\mathbf{q}$,即
在推理时,对查询$q$ 的嵌入向量执行最近邻搜索,在嵌入向量空间中寻找可能满足查询的节点。
生成嵌入向量 $\mathbf{q} $
将query用其DAG依赖图表示
依赖图中包含anchor nodes和variable nodes和他们之间的边。其中查询目标为唯一的 汇聚节点
从其中anchor nodes的嵌入向量$\mathbf{z}_{v1} ,\cdots,\mathbf{z}_{vn}$ 开始,用$\mathcal{P, L}$ 从这些嵌入向量中计算$\mathbf{q}$
$\mathcal{P}$ 算子
给定query的嵌入向量$\mathbf{q}$ 和边的类型$\tau$,几何投影(Projection)算子输出一个新的query嵌入向量$\mathbf{q’} = \mathcal{P}(\mathbf{q},\tau)$,相应的表示为$[q’]= \bigcup_{v \in [q]} \ N(v,\tau)$,其中$N(v,\tau)$ 表示和节点$v$ 通过$\tau$ 类型的边连接的节点集。
$\mathcal{P}$ 接收一个对应于节点集[q]的嵌入向量,输出一个对应于和其以$\tau$ 连接的节点集的嵌入向量。
$\mathcal{P}(\mathbf{q},\tau) = \mathbf{R_\tau q}$
其中$\mathbf{R_\tau^{d\times d}}$ 是边类型$\tau$ 的可训练参数矩阵。
$\mathcal{L}$ 算子
给定具有相同的输出节点类型$\gamma$ 的query的嵌入向量集$\mathbf{q_1},\cdots,\mathbf{q_n}$,几何交集(Intersection)算子输出一个新的嵌入向量$\mathbf{q’}$,对应于$[q’]=\bigcap_{i=1,\cdots,n}\ [q]_i$ ,在嵌入空间执行交集。
$\mathcal{L}(\{\mathbf{q_1},\cdots,\mathbf{q_n}\})=\mathbf{W}_\gamma\Psi(\mathbf{NN_k(q_i)},\forall i=1,\cdots,n)$
$\mathbf{NN_k}$ 是一个k层的前馈神经网络,$\Psi$ 是对称的向量函数,$\mathbf{W}_\gamma$ 是可训练的对每个节点类型$\gamma \in \Gamma$的变换矩阵
用$\mathcal{P,L}$算子推理
为了生成query的嵌入向量,首先根据anchor nodes的出边对其嵌入向量投影($\mathcal{P}$)。
如果一个节点在query的DAG中有多个入边,用$\mathcal{L}$ 算子聚合传入的信息。
然后重复这个过程直至到达query的目标。
节点embedding
原则上,任何生成节点embedding的有效可微算法都可以用,本文中用了标准的”bag-of-features”方法,假设每一个类型为$\gamma$ 的节点都有一个相关的二值特征向量$\mathbf{x}_u \in \mathbb{Z}^{m_\gamma}$,计算embedding的方法如下:
$\mathbf{z}_u = \mathbf{\frac{Z_\gamma X_u}{|X_u|}}$
其中$\mathbf{Z_\gamma}$ 是可训练的embedding矩阵,$\mathbf{x_u}$ 是独热指示向量。