论文阅读: Reasoning on Knowledge Graphs with Debate Dynamics

论文链接：Reasoning on Knowledge Graphs with Debate Dynamics

主要思路是（1）对给定的query三元组，用强化学习的方法，两个agent分别寻找论证true和false的证据链；（2）Judge以二分类器评估两个Agent寻找的证据链中的每条证据，并给予Reward。

[TOC]

Abstract

提出了基于辩论动力学的知识图谱自动推理方法。将三分类任务构建为一个两个强化学习系统间的辩论游戏。两个Agent以论证为目标抽取知识图谱中的路径，为正题或反题提供可解释证据。工作的重点是创建一种可解释的方法以保持高预测准确率。

1. Introduction

KG以三元组$(s,p,o)$表示，subject 和 object对应图中的节点，predicate对应连接两者的边。KG中的节点表示现实世界实体，谓词描述实体对关系。

KG的主要问题是 大多数KG是不完整的/包含虚假事实的。针对该问题的一些机器学习算法致力于通过观察连通性模式来推断缺失的三元组或检测虚假事实。此外，问答和协同过滤任务等也可以通过预测连接来完成。大多数算法都将实体与谓词嵌入到低维向量空间中，然后根据这些嵌入值计算三元组的置信度得分。大多数基于嵌入的方法都具有黑箱特性——对用户隐藏了导致这个分数的因素。

大多数可解释的AI方法可以分为两种：因果解释能力和综合透明度，前者旨在揭示已经训练好的黑箱模型输出；综合透明度方法使用内部解释机制或因为模型复杂度低而自然可解释。而低复杂性和预测精度经常是相互冲突的。本文的目标是设计一种综合透明方法，兼顾效率和用户参与。

本文提出了基于强化学习的方法，受前人提出的通过debate提高AI安全性的概念启发。两个Agent对三元组提出论点进行判断，judge（二分类器）决定最终的真假。与大多数表示学习的方法相反，这些论点对用户可见，用户可以追溯judge的分类，并可以否决器决定。因此，R2D2的综合透明机制是基于可解释特征的自动提取而非低复杂度。

2. Background

$$\mathcal{KG \subset E \times R \times E,\ E为实体集, \ R为关系集}$$

为了表明一个三元组的真假，引入二值特征函数 $\phi : \mathcal{E \times R \times E} \rightarrow \{0,1\}$

$\phi(s,p,o)=1$ 即该三元组为真。如果KG中没有包含某三元组，则该三元组未知而非错误（开放世界假设）。KG推理主要分为以下两个任务：

• 缺失三元组的推理
• 预测三元组的truth value

本文中triple classification指预测truth value即$\phi(s,p,o)$，而KG completion指评估$o \in \mathcal{E}$与$(s,p) \in \mathcal{E \times R}$对形成真三元组的可能。

表示学习在KG中的基本思想是把实体和关系投影到一个低维向量空间中，然后将三元组的likelihood作为embedding空间上的函数来建模。Das et al. 提出了与本文相关的的多跳推理方法MINERVA，基本思想是向Agent显示查询的subject和predicate，让它们执行策略引导的walk以找到正确的object，产生的路径也具有一定的可解释性。

3. Method

根据两个对立的Agent间的辩论进行三元组分类，因此查询三元组至关重要（辩论中心）。Agent不断挖掘KG上可作为证据（正或反）的路径，即按顺序遍历图，根据过去的转换和查询三元组决定下一跳，并将该转换扩展到当前路径。所有路径都由一个judge分类器区分真假，步骤归纳如下：

• 查询三元组被提供给两个Agent
• 两个Agent轮流从KG中提取证据路径
• judge处理证据和查询三元组，评估三元组的truth value

States 每个Agent的状态空间为$\mathcal{S:E^2 \times R \times E} $，被表示为$S^{(i)}_t = (e^{(i)}_t,q),q=(s_q,p_q,o_q)，i \in \{1,2\}$，其中q为query三元组。

Actions 某状态下可采取的行动集$\mathcal{A_{S^{(i)}_t}}$，由所有$e^{(i)}_t$的出边和对应的目标节点组成，包括自循环。

Environments 环境根据Agent的Actions更新State。$\delta^{(i)}_t(S^{(i)}_t ,A^{(i)}_t) := (e^{(i)}_{t+1},q),S^{(i)}_t = (A^{(i)}_t,q),A^{(i)}_t = (r,e^{(i)}_{t+1})$

Policies 用$H^{(i)}_t = (H^{(i)}_{t-1},A^{(i)}_{t-1})$ 表示Agent i到时间t的历史路径，其中$H^{(t)}_t = (s_q,p_q,o_q)$。用LSTM网络对其编码得到：

$$h^{(i)}_t = LSTM^{(i)}([a^{(i)}_{t-1}, q^{(i)}]) \tag{1}\\其中a^{(i)}_{t-1}=[r^{(i)}_{t-1},e^{(i)}_t] \in \mathbb{R}^{2d}, q^{(i)}=[e^{(i)}_s,r^{(i)}_p,e^{(i)}_o] \in \mathbb{R}^{3d}$$

$a^{(i)}_{t-1}$ 表示前一个action，$r^{(i)}_{t-1},e^{(i)}_t$ 表示关系和目标实体的嵌入向量embedding，LSTM的输入应该是5个长度为d的向量。$q^{(i)}$ 对query三元组编码，每个Agent和judge的嵌入向量都是不同的，即每个节点、边有三个嵌入向量。

每个Agent 根据历史信息和待选择的actions计算每个action的得分：

$$d^{(i)}_t = softmax(A^{(i)}_t(W^{(i)}_2 ReLU(W^{(i)}_1 h^{(i)}_t))) \tag{2} \\ 其中A^{(i)}_t \in \mathbb{R}^{|A_{S^{(i)}_t}| \times d}包括S^{(i)}_t 状态下的所有潜在action$$

此处$d^{(i)}_t$ 的分量表示选择actions中各action的概率，根据此概率概率采样选择下一action。

$$A^{(i)}_t \sim Categorical(d^{(i)}_t) \tag{3}$$

这一策略是马尔可夫决策过程，仅考虑了t-1步的策略和t步的actions空间，与之前的信息无关。上述（1）和（2）定义了从历史信息到actions空间的映射，从而产生了策略变量$\pi_{\theta^{(i)}}$，$\theta^{(i)}$ 是等式中的可训练参数。

Debate Dynamics 对第一步中两个Agent产生的结果进行辩论。以固定的轮数N，在每轮中两个Agent从$s_q$ 以固定的路径长遍历图，judge观察Agents的路径，对三元组做出预测。Agent 1根据式（1）-（3）产生包含states和actions的长度为T的序列，然后Agent 2产生类似的序列。algorithm 1

每个Agent采样得到N个证据链，第n次采样得到的证据为：

$$\tau_n^{(i)} := (A_{\overline n(i,T)+1},A_{\overline n(i,T)+2},\cdots,A_{\overline n(i,T)+T}) \tag{4} \\ 下标定义为 \overline n(i, T) := (2(n−1)+i−1)T.$$

结果汇总为：

$$\tau := (\tau_1^{(1)},\tau_1^{(2)},\tau_2^{(1)},\tau_2^{(2)},\cdots,\tau_N^{(1)},\tau_N^{(2)}) \tag{5}$$

The Judge R2D2中Judge有双重功能：

• 二分类器，鉴别真伪事实
• 评估Agents的证据质量，并给予奖励，从而引导Agents产生有意义的证据

judge通过前馈神经网络分别处理每个证据，将输出求和得到二分类器的结果：

$$y_n^{(i)} = f ([\tau _n^{(i)}, q^J]) \tag{6}$$ $$\tau _n^{(i)} := [a_{\overline n(i,T)+1}^J,a_{\overline n(i,T)+2}^J,\cdots,a_{\overline n(i,T)+T}^J] \tag{7}$$

其中$a_t^J = [r_t^J, e_t^J] \in \mathbb{R}^{2d}$ 表示Judge对$A_t$ 的嵌入向量embedding，$q^J = [r_p^J, e_o^J] \in \mathbb{R}^{2d}$ 表示Judge对query中predicate和object的嵌入向量embedding。处理完所有证据后，Judge根据$t_\tau \in (0,1)$ 评判查询三元组q：

$$t_\tau = \sigma (w^TReLU(W \Sigma_{i=1}^2 \Sigma_{n=1}^N y_n^{(i)})) \tag{8}$$

其中$w$ 表示可训练参数，$\sigma$ 表示sigmoid函数。

通过交叉熵loss给出了judge的目标函数：

$$\mathcal L_q = \phi (q) log\ t_\tau + (1-\phi(q))(1-log\ t_\tau) \tag{9}$$

R2D2的总体架构如下图所示：

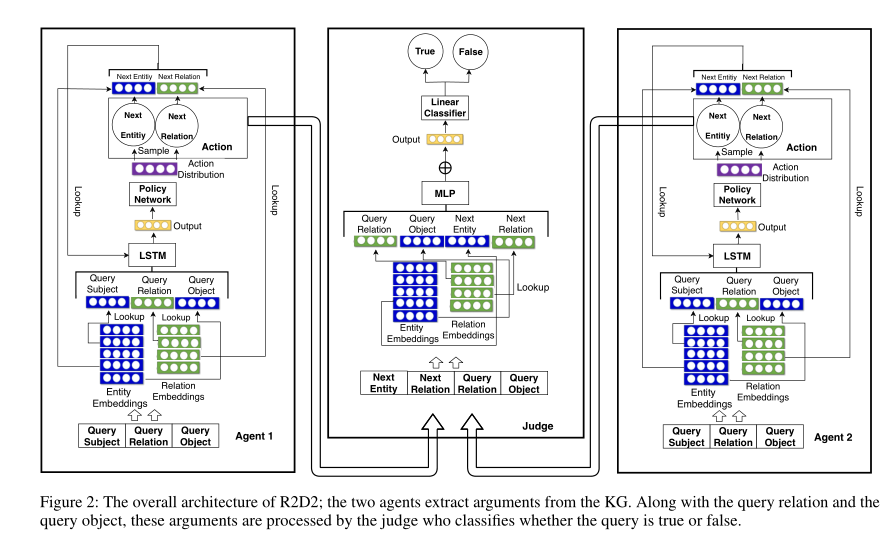
Rewards

为了体现两个Agent工作的不同，judge对每个证据分别计算每个Agent的得分：

$$t_n^{(i)} = w^TReLU(Wf ([\tau _n^{(i)}, q^J])) \ \ (11)$$

$t_n^{(i)}$ 只和Agent i的第n轮证据有关，奖赏函数为：

$$R_n^{i} = \begin{cases} t_n^{(i)}, & \text{if i = 1} \\ -t_n^{(i)}, & \text{otherwise} \end{cases} \tag{12}$$

Reward Maximization and Training Scheme

Agent的累计奖赏为：

$$G^(i) := \Sigma_{n=1}^N R_n^{(i)} \tag{13}$$

用强化学习的思想最大化累计奖赏的期望以训练Agent：

$$\mathop{argmin} \limits_{\theta^{(i)}} \mathbb{E}_{q \sim \mathcal{KG+}} \mathbb{E}_{\tau_1^{(i)},\tau_2^{(i)},\cdots,\tau_N^{(i)} \sim \pi_{\theta^{(i)}}}[G^{(i)} | q] \tag{14}$$

其中$\mathcal{KG+}$ 是训练三元组，除了包含KG中三元组外，还包含未观察到的三元组。通常会通过将正确三元组$(s,p,o)$ 中的$o$ 替代为空来创建负例。但本文中采用了生成看似合理但却错误的三元组的方法：对$(s,p,o)\in \mathcal{KG}$ 生成一个$(s,p,\widetilde o) \notin \mathcal{KG}$，但$\widetilde o$出现在$p$相关的其他关系中，即$\mathcal{KG}_C := \{(s,p,\widetilde o) | (s,p,\widetilde o) \notin \mathcal{KG},\exist \widetilde s:(\widetilde s,p,\widetilde o) \in \mathcal{KG}\}$。这种方法不会在破坏隐形约束的三元组上浪费资源。

模型的训练采用交替训练方案，一次只训练Agent或Judge。

code

出现提示

WARNING:tensorflow:Entity <bound method TensorFlowOpLayer._defun_call of <tensorflow.python.eager.function.TfMethodTarget object at 0x000001805B549780>> could not be transformed and will be executed as-is. Please report this to the AutoGraph team. When filing the bug, set the verbosity to 10 (on Linux, `export AUTOGRAPH_VERBOSITY=10`) and attach the full output. Cause: Bad argument number for Name: 3, expecting 4

需要安装低版本gast

pip install gast==0.2.2